replace inv and det for 4x4 matrices, #260

TsurHerman · 2017-07-29T13:50:23Z

Added inv and det for 4x4 matrix size , as a stopgap until a more compact representation is found.

coveralls · 2017-07-29T14:00:53Z

Coverage decreased (-0.2%) to 88.987% when pulling a0d168f on TsurHerman:pull-request/a0d168f3 into da1a371 on JuliaArrays:master.

TsurHerman · 2017-07-30T09:53:26Z

Failure is in 32bit systems due to fact that implicit conversion to float is to Float32.
This affects accuracy of badly conditioned 4x4 matrices on 32 bit systems.
I think this test can be relaxed.

What do you recommend?

mschauer · 2017-07-30T10:17:13Z

implicit conversion to float is to Float32

Can you be more specific what is going on? There is no Float, only Float32 and Float64 (unlike Int, Int32, Int64) because also 32 bit systems have Float64.

TsurHerman · 2017-07-30T11:38:46Z

inv. and det for 4x4 do not specify type explicitly but instead rely on the system automatic promotion
in expressions such as:
A[13] * A[10] * A[7] * A[4] - A[9] * A[14] * A[7] * A[4]

for x64 bit systems the test for ill conditioned matrix of size 4x4 passes
norm(Matrix(inv(sm)*sm - eye(4))) < 10*norm(inv(m)*m - eye(4))
on x32 bit systems it fails, by not much by the way.
Best course of action would be to relax the test.

EDIT:

the original test was :@test_broken , that is, was supposed to fail on all systems.
after this PR , the test passes but only on x64 systems

mschauer · 2017-07-30T11:47:42Z

I think I am specifically curious which promotions go different on 32 systems.

TsurHerman · 2017-07-30T12:24:12Z

I may have a 32 bit system behind my facsimile sitting on top of my laser-disc ... no its not there anymore. :-)

I agree it is interesting(it might have implications on embedded systems), but I can't help with that.

fredrikekre · 2017-07-30T12:32:30Z

The test is with a Float64 matrix even on 32bit, so should not be promotion that is the problem.

mschauer · 2017-07-30T12:34:47Z

Yes, that is what I thought, but wasn't sure about. But it is not a catastrophic loss of accuracy anyway, replacing 10* by 12* would be a simple solution.

coveralls · 2017-07-30T12:59:26Z

Coverage decreased (-0.04%) to 89.101% when pulling 02b4890 on TsurHerman:pull-request/a0d168f3 into da1a371 on JuliaArrays:master.

codecov-io · 2017-07-30T13:05:56Z

Codecov Report

Merging #260 into master will increase coverage by 3.25%.
The diff coverage is 100%.

@@            Coverage Diff             @@
##           master     #260      +/-   ##
==========================================
+ Coverage   89.38%   92.63%   +3.25%     
==========================================
  Files          36       36              
  Lines        2629     2622       -7     
==========================================
+ Hits         2350     2429      +79     
+ Misses        279      193      -86

Impacted Files	Coverage Δ
src/inv.jl	`100% <100%> (ø)`	⬆️
src/det.jl	`100% <100%> (ø)`	⬆️
src/eigen.jl	`91.47% <0%> (-0.76%)`	⬇️
src/mapreduce.jl	`100% <0%> (ø)`	⬆️
src/broadcast.jl	`100% <0%> (ø)`	⬆️
src/indexing.jl	`86.55% <0%> (+0.53%)`	⬆️
src/MArray.jl	`96.27% <0%> (+1.24%)`	⬆️
src/SArray.jl	`96.55% <0%> (+1.99%)`	⬆️
src/SMatrix.jl	`94.78% <0%> (+2.54%)`	⬆️
src/linalg.jl	`99.47% <0%> (+2.61%)`	⬆️
... and 14 more

Continue to review full report at Codecov.

Legend - Click here to learn more
Δ = absolute <relative> (impact), ø = not affected, ? = missing data
Powered by Codecov. Last update 79ac5f1...801b43c. Read the comment docs.

ChrisRackauckas · 2017-08-02T06:28:47Z

Just chiming in since I was pointed here by @mschauer. Yes, AppVeyor 32-bit seems to apply different optimizations than 64-bit. We found this by very carefully comparing a whole bunch of different algorithms, and found some very small differences even when some macros were removed.

SciML/DelayDiffEq.jl#20
SciML/DelayDiffEq.jl#22

As @fredrikekre points out:

The test is with a Float64 matrix even on 32bit, so should not be promotion that is the problem.

Both 32-bit and 64-bit use Float64, bit only refers to integer size. So it really is likely due to differences beyond your control, and not due to any type promotions.

c42f · 2017-08-02T10:42:17Z

test/inv.jl

-    @test_broken norm(Matrix(inv(sm)*sm - eye(4))) < 10*norm(inv(m)*m - eye(4))
-    @test_broken norm(Matrix(sm*inv(sm) - eye(4))) < 10*norm(m*inv(m) - eye(4))
+    @test norm(Matrix(inv(sm)*sm - eye(4))) < 12*norm(inv(m)*m - eye(4))
+    @test norm(Matrix(sm*inv(sm) - eye(4))) < 12*norm(m*inv(m) - eye(4))


These tests were particularly chosen as examples where the previous implementation had trouble. So they're probably not that relevant to the new implementation.

Presumably we'd be able to find some equivalent problems by rerunning the code at the bottom of this file.

This is still a difficult case (as evidenced by the bounds being quite tight). But running the problem generator would be a good idea.

c42f · 2017-08-02T10:47:00Z

test/inv.jl

-    @test norm(Matrix(sm*inv(sm) - eye(4))) < 10*norm(m*inv(m) - eye(4))
-    @test norm(Matrix(inv(sm)*sm - eye(4))) < 10*norm(inv(m)*m - eye(4))
+    @test norm(Matrix(sm*inv(sm) - eye(4))) < 12*norm(m*inv(m) - eye(4))
+    @test norm(Matrix(inv(sm)*sm - eye(4))) < 12*norm(inv(m)*m - eye(4))


This change is ok I think. There's nothing special about the factor of 10 which you've replaced with 12 here. I'd say some difference is to be expected with a switch in algorithms.

c42f

Thanks for fixing this. I noticed one extra change which we should add regarding similar_type. Other than that, we should be good to go here.

c42f · 2017-08-04T06:35:04Z

src/inv.jl

+        (A[1,3]*A[2,4]*A[3,1] - A[1,4]*A[2,3]*A[3,1] + A[1,4]*A[2,1]*A[3,3] - A[1,1]*A[2,4]*A[3,3] - A[1,3]*A[2,1]*A[3,4] + A[1,1]*A[2,3]*A[3,4]) * idet
+        (A[1,4]*A[2,2]*A[3,1] - A[1,2]*A[2,4]*A[3,1] - A[1,4]*A[2,1]*A[3,2] + A[1,1]*A[2,4]*A[3,2] + A[1,2]*A[2,1]*A[3,4] - A[1,1]*A[2,2]*A[3,4]) * idet
+        (A[1,2]*A[2,3]*A[3,1] - A[1,3]*A[2,2]*A[3,1] + A[1,3]*A[2,1]*A[3,2] - A[1,1]*A[2,3]*A[3,2] - A[1,2]*A[2,1]*A[3,3] + A[1,1]*A[2,2]*A[3,3]) * idet]
+        return SMatrix{4,4,eltype(B),16}(B)


The return type here should arguably be deduced using similar_type rather than always returning SMatrix. See, for example, the implementations of _inv for the smaller sizes.

The idea here is that users can preserve the container type of their static matrix if they so please. I'm not sure this is used a lot in practice, but best for consistency to keep the same pattern.

Agreed , waiting for my pull request regarding det.jl to be merged into master, since there are additional small fixes,and then I will merge back master here and change it to be consistent (adding the similar_type instead of SMatrix)

Updated everywhere to return similar_type and not SMatrix

# Conflicts: # src/det.jl # test/det.jl

coveralls · 2017-08-05T07:34:10Z

Coverage decreased (-0.08%) to 89.234% when pulling cc34e5e on TsurHerman:pull-request/a0d168f3 into 79ac5f1 on JuliaArrays:master.

andyferris · 2017-08-06T06:29:13Z

src/det.jl

 end

+@inline function _det(::Size{(4,4)}, A::StaticMatrix,S::Type)
+    A = similar_type(A,S)(A)


There used to be compiler (type inference) problems with variable names that change types. Has this been fixed? (I.e. is code optimal here when eltype(A) != S?)

yes there is a difference , it is not big (about 2 ns difference) , but the code produced if
we avoid variable name changing type looks better .it looks like what you would expect hand optimized assembly code would look like, a long list of vector intrinsics.

Any preferred style?

I thought of changing each function that this line appears as the first line in this way:

@inline function _det(::Size{(3,3)}, A::StaticMatrix, S::Type) A = similar_type(A,S)(A)

would become:

@inline function _det(::Size{(3,3)}, _A::StaticMatrix, S::Type) A = similar_type(_A,S)(_A)

Or move the promoting to the dispatching function all together and dropping the propagation of the promoted type.
Better in my opinion

@andyferris Both will work , what style do you prefer?

By now, I am used to the "SSA" form so I do tend to write a2 = f(a); a3 = g(a2) etc. In this case something like A_S would look clear.

Dispatch might be a very clean solution - the line won't even appear when S is already correct, which may be important for e.g. heap allocated static arrays or if similar_type always changes types or if the compiler doesn't optimize away the construction for some reason.

So let's try dispatch!

…ction

coveralls · 2017-08-07T06:53:52Z

Coverage increased (+0.7%) to 90.034% when pulling e578b9b on TsurHerman:pull-request/a0d168f3 into 79ac5f1 on JuliaArrays:master.

TsurHerman · 2017-08-07T18:06:14Z

@c42f your requested changes are in place, similar_type instead of SMatrix
besides that moved the type promotion to the dispatching function.
So if you first merge this PR and then yours about logdet .. then I think this covers everything.

det inv and logdet give correct result in a speedy manner for matrices of small size up to size 4 with any type that Base supports including integer and unsigned , and calls Base on large matrices

andyferris · 2017-08-08T03:22:07Z

src/inv.jl

    T = eltype(A)
    S = typeof((one(T)*zero(T) + zero(T))/one(T))
-    newtype = similar_type(A, S)
+    A_S = similar_type(A,S)(A)


A_S = convert(similar_type(A, S), A)

andyferris · 2017-08-08T03:22:28Z

src/det.jl

    T = eltype(A)
    S = typeof((one(T)*zero(T) + zero(T))/one(T))
-    _det(Size(A),A,S)
+    A_S = similar_type(A,S)(A)


A_S = convert(similar_type(A, S), A)

Can potentially remove a new allocation of e.g. a MMatrix.

I dont see that changes anything , but I am updating anyway

And the biggest problem is that inv for MMatrix returns SMatrix

coveralls · 2017-08-08T16:01:01Z

Coverage increased (+1.3%) to 90.592% when pulling 045c1cf on TsurHerman:pull-request/a0d168f3 into 79ac5f1 on JuliaArrays:master.

TsurHerman · 2017-08-12T12:09:07Z

Hi guys, any chance that this is getting in soon?
@c42f can you approve your requested changes?

c42f · 2017-08-18T19:49:48Z

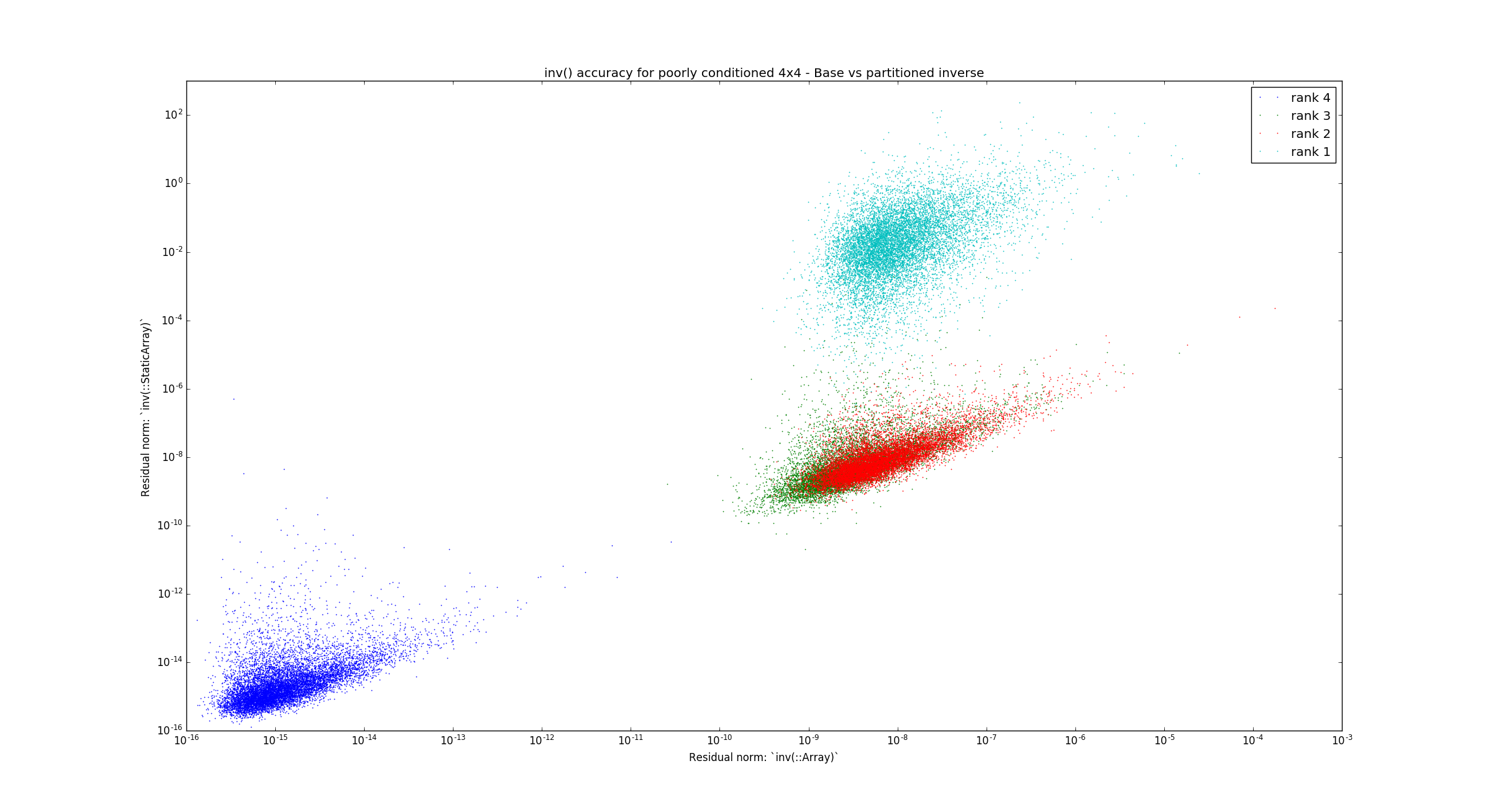
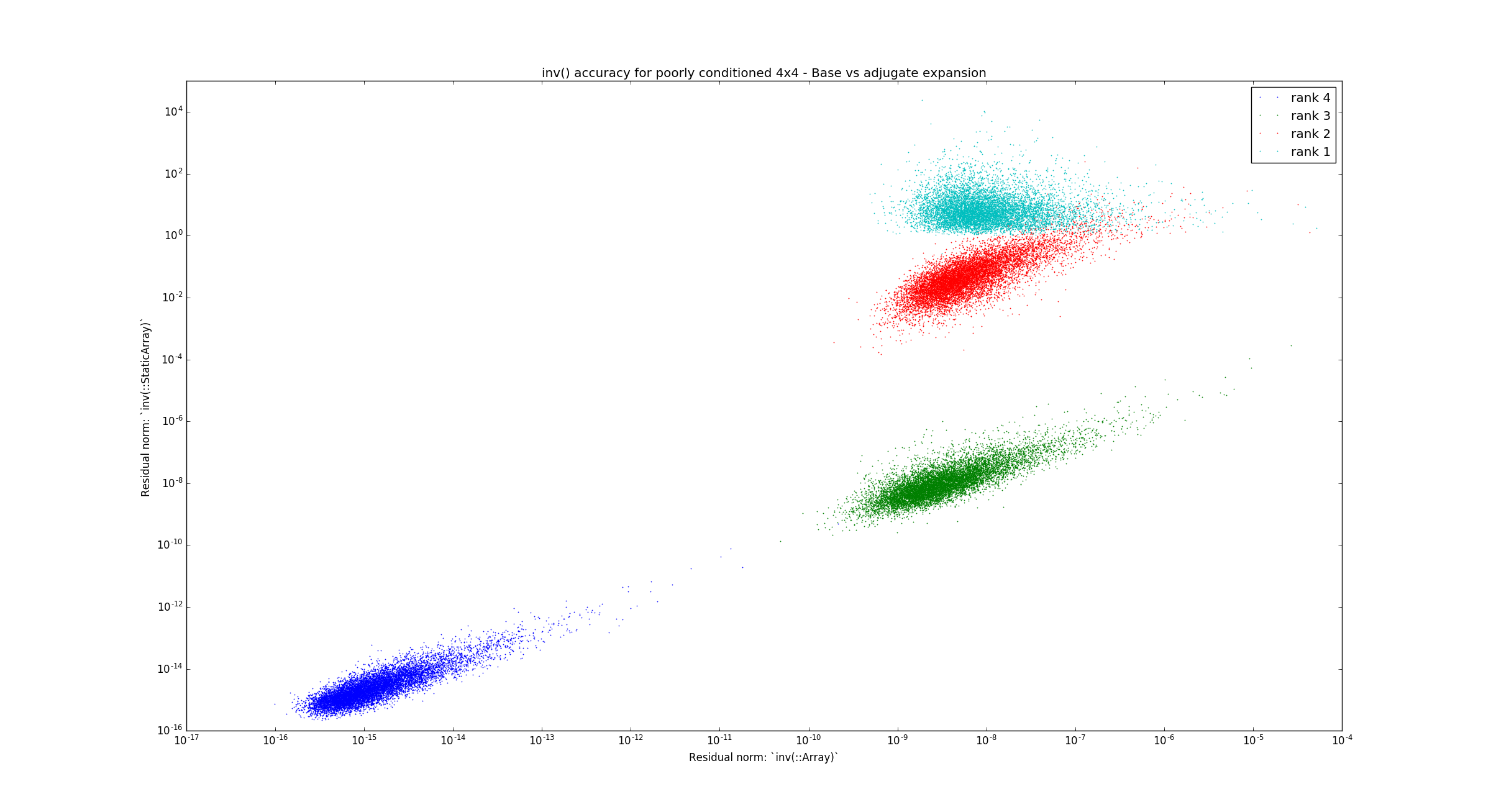
Ah, this one slipped off my radar. Looks good now thanks.

@mschauer I did rerun the problem generator, and it produced the following graphs which compare the two different methods of computing the 4x4 inverse with the Base implementation:

Partitioning method (previous)

Adjugate method (changes here)

So clearly the new method behaves more robustly for well conditioned matrices (the dark blue blob is tight). If nothing else, it's clear we need to do this well, so I think this is a reasonable tradeoff for now.

The new method does have some has some systematic problems for approximately low ranked matrices, where if fares a lot worse than the previous method. We'll just have to put up with that for now.

c42f · 2017-08-18T20:06:49Z

Oh, we should really add the test case which kicked all this off - the 4x4 permutation matrix from #250. I'll do this now.

c42f · 2017-08-18T20:09:41Z

Ok, I added that test case. Let's merge this as soon as CI has passed.

coveralls · 2017-08-18T20:47:45Z

Coverage increased (+3.3%) to 92.639% when pulling 801b43c on TsurHerman:pull-request/a0d168f3 into 79ac5f1 on JuliaArrays:master.

* Turn off struct broadcast by default. * add doc and rename * Add more unalias test. * Also overload `instantiate` and `_axes` This makes sure `Tuple`'s axes static during struct static broadcast. * Update wording --------- Co-authored-by: Pietro Vertechi <[email protected]>

replace inv and det for 4x4 matrices,

a0d168f

TsurHerman mentioned this pull request Jul 29, 2017

Bug in inverse of 4x4 matrix returning NaN #250

Closed

Relax test for poorly conditioned 4x4 matrices

02b4890

andyferris approved these changes Aug 1, 2017

View reviewed changes

c42f reviewed Aug 2, 2017

View reviewed changes

c42f requested changes Aug 4, 2017

View reviewed changes

TsurHerman added 4 commits August 5, 2017 09:32

Merge branch 'master' into pull-request/a0d168f3

6301885

# Conflicts: # src/det.jl # test/det.jl

Make inv similar to det and clear noise

0cd325a

speed improvement for 2x2 inv

3fbb854

similar_type convert on all inv methods including >4 and 1

cc34e5e

andyferris reviewed Aug 6, 2017

View reviewed changes

Avoid variable name changing type, moved promotion to dispatching fun…

e578b9b

…ction

andyferris reviewed Aug 8, 2017

View reviewed changes

explicitly call convert instead of constructor

045c1cf

c42f approved these changes Aug 18, 2017

View reviewed changes

mschauer approved these changes Aug 18, 2017

View reviewed changes

Add a 4x4 permutation matrix as an inv() test

801b43c

c42f merged commit 922247e into JuliaArrays:master Aug 18, 2017

snoeyink mentioned this pull request Jun 22, 2022

Rewrite 4x4 det as product of 2x2 minors for improved performance #1046

Merged

replace inv and det for 4x4 matrices, #260

replace inv and det for 4x4 matrices, #260

Uh oh!

Conversation

TsurHerman commented Jul 29, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Uh oh!

coveralls commented Jul 29, 2017

Uh oh!

TsurHerman commented Jul 30, 2017

Uh oh!

mschauer commented Jul 30, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Uh oh!

TsurHerman commented Jul 30, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Uh oh!

mschauer commented Jul 30, 2017

Uh oh!

TsurHerman commented Jul 30, 2017

Uh oh!

fredrikekre commented Jul 30, 2017

Uh oh!

mschauer commented Jul 30, 2017

Uh oh!

coveralls commented Jul 30, 2017

Uh oh!

codecov-io commented Jul 30, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Codecov Report

Uh oh!

ChrisRackauckas commented Aug 2, 2017

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

c42f left a comment

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

coveralls commented Aug 5, 2017

Uh oh!

andyferris Aug 6, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

TsurHerman Aug 6, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Choose a reason for hiding this comment

Uh oh!

TsurHerman Aug 6, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Choose a reason for hiding this comment

Uh oh!

andyferris Aug 6, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Choose a reason for hiding this comment

Uh oh!

coveralls commented Aug 7, 2017

Uh oh!

TsurHerman commented Aug 7, 2017 • edited Loading Uh oh! There was an error while loading. Please reload this page.

Uh oh!

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

Uh oh!

Choose a reason for hiding this comment

TsurHerman commented Jul 29, 2017 •

edited

Loading

mschauer commented Jul 30, 2017 •

edited

Loading

TsurHerman commented Jul 30, 2017 •

edited

Loading

codecov-io commented Jul 30, 2017 •

edited

Loading

andyferris Aug 6, 2017 •

edited

Loading

TsurHerman Aug 6, 2017 •

edited

Loading

TsurHerman Aug 6, 2017 •

edited

Loading

andyferris Aug 6, 2017 •

edited

Loading

TsurHerman commented Aug 7, 2017 •

edited

Loading

TsurHerman commented Aug 12, 2017 •

edited

Loading